見習い大工の内田です。
先週に金、土曜日と二日間で学校の実技がありました。
今回の課題は「四方転びの踏み台」です。
四方転びとは四方の柱が中央に向かって傾斜した形状を言います。
四方転びにすることで真っすぐの時よりも安定し主に寺の鐘楼や神社の水屋などに使われます。
この四方転びのを半分にしたものが今回の課題です。
今回の課題は今の2級大工技能士の課題です。
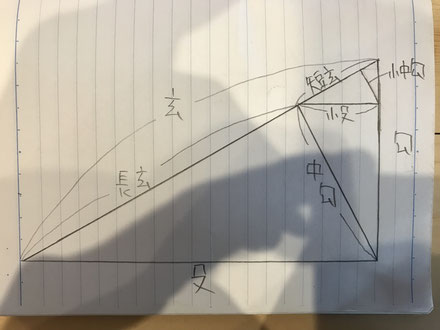
今回の課題を作るにあたって始めに原寸図を描くのですがその時に勾股玄の定理というものを使います。
勾股玄の定理とは直角三角形の三辺に関する定理で勾は直角三角形の短辺、股は長編、玄は斜辺のことを表しています。
勾股玄の定理=三平方の定理です。
この直角三角形に自在に線を出していくことで四方転びで使う勾配を出します。
四方転びでは柱が四方に広がっていので柱の設置面を正方形にするためには断面をひし形に加工しないといけません。
このひし形にするための角度も上の基本図にさらに線を加えていけば長さが取ることができるようになります。
柱をつなぐための貫や柱を入れる天板のホゾ穴は真っすぐに掘るのではなく柱の勾配と同じに斜めに掘らないといけません。
今回の課題でほぞ穴は全部で8つあるのですがそのうち勾配がなく掘るものは2つだけです。
刻みも同じく勾配があり勾配通りに切るのは難しいです。
加工が終わり組立ましたが穴の勾配が少し広がってしまっていて足が外に開いてしまいました。
次回も同じく四方転びなので今回よりも精度をあげられるように頑張りたいと思います。